True-positive rate and false-positive rate

Karen Tao, Researcher
February 17, 2021

In my last blog post, we looked at a confusion matrix created to evaluate the accuracy of a machine learning model built to classify whether a gift was liked. We will continue to explore two more important measures with that foundation before concluding our series of accuracy measures for classification machine learning models: true positive rate and false-positive rate.

Some of the most common classification models include naive Bayes and logistic regression. These are probabilistic models, meaning the models calculate the probability of an event happening. In my previous gift-giving example, the model provides the probability of 200 gifts that were liked. More specifically, the model may predict the probability of a doll being liked to be 0.68, and the model calculates these prediction probabilities for each of the 200 gifts. Each gift would end up with a different prediction probability between 0 and 1. Recall that probability is always a value between 0 and 1, 0 being impossible and 1 being a certainty.

How does the model turn this numerical probability value into a categorical yes/no output? That is where a threshold comes into play. If we have an evenly distributed dataset, we could set this threshold to 0.5 so that the model predicts "yes" if the probability is greater than 0.5; the machine predicts "no" otherwise. The doll with a prediction probability of 0.68 would be classified as "yes" in this case. In the real world, we may not always have an evenly distributed dataset.

Remember my niece who used to say "No" to everything? In those cases, we could set our threshold to be higher than 0.5. Let us say we set our threshold to 0.7. The doll with a prediction probability of 0.68 would be classified as "No" this time since it does not cross the threshold. This scenario mirrors my niece's preferences more closely since our model with the higher threshold correctly predicted she would not like the gift. Below is an example of what outputs may look like for different thresholds of our gifts.

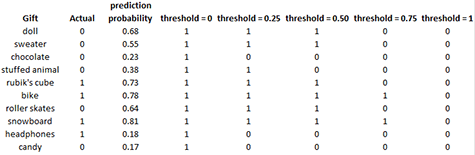
This table uses the common binary expression 1 to indicate "Yes" and 0 to indicate "No." For the doll that my niece did not like, the model predicted a probability of 0.68 of her liking it. The model would output "yes" for thresholds 0, 0.25, and 0.50. The model would output "no" for thresholds 0.75 and 1 since the predicted probability does not cross the two higher thresholds. We can see the numbers of true positive and false positive predictions change significantly depending on which threshold was chosen, even when we look at only ten gifts. The confusion matrices for each of the thresholds would be different as a result.

Using the different confusion matrices, we can calculate the true positive rate (TPR) and the false positive rate (FPR) for each of our classifier's threshold values. We defined the true positive rate in our last post: the number of true positives over the number of ground truth positives. The false-positive rate is the number of false positives over ground truth negatives. Below are the formulas for TPR and FPR.

Now that we have defined TPR and FPR, our stage is set to introduce the AUC-ROC curve. Stay tuned for my next blog post to learn more about the intuition behind how to interpret this popular tool.